皆さん普段の仕事の中で角度計算や三角形の辺の長さ計算てしてますか？

関数電卓でやっってますよ～

CAD使って計算します～

いやいや、今の時代は携帯のアプリっしょ！

アプリでなんて古い人間（私も・・・）からみたら大丈夫？と思うでしょうが

意外とこれが図形を見ながら直接入力なので簡単なのですよ

画面タッチですから　こんな図形で

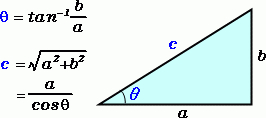
勿論、関数電卓をお使いの方で有ればおなじみの図形ですね

角度θを出すのに必要な図形（図では「の直角マークが抜けてますが直角三角形が条件です）

例えば辺ｃと辺ｂの長さがわかれば角度θが出せます

辺aと辺ｃでも、辺aと辺ｂでも

つまり2辺の長さがわかれば角度θは出せます

逆に角度θと辺a・b・cの何れかの長さ1辺がわかれば残り2辺の長さは求められます。辺ｃの√での求め方の数式は学校でも習ったと思います（私は記憶に御座いませんが・・・）

1番目と3番目の数式は関数電卓を使う方は必ず通る式ですね。

sin（サイン） cos（コサイン） tan（タンジェント）

辺の長さがわかっていて計算する時にどっちをどっちで割るの？

ってなると悩む時有りませんか？

その時に覚えて損が無いのがｓとｃとｔの小文字の筆記体です

ｓの筆記体は左下から右上に上がって下がりますよね。

（辺ｃから辺ｂへ書くイメージ）

ｃはそのまま反時計回りに円弧を描く様に書きます

（辺ｃからへんａへ書くイメージ）

ｔは左下から右上に上がって下がりますよね

（辺ａから辺ｂへ書くイメージ）

これをそのまま図形に当てはめるのです。

最初が分母で次が分子

辺ｃと辺ｂがわかっているならsinを使って計算となります。

その時の書き順がそのまま分母・分子に当てはまります

つまりcが分母bが分子と

b÷c　にsin⁻¹をかけてやればよいのです

（実際の電卓操作はメーカーにより異なりますよー）

cとaならa÷c　cos-¹

aとbならb÷a　tan-¹

必ず図形の配置は右に直角で上の角度にsin、左の角度にcos、右の直角にtan

を使うのです。

数学ですから　数式を変えれば別の部分を求める事が出来ます。

aとθがわかっていれば　bもcも出せます

bとθがわかっていれば　aもcも出せます

cとθがわかっていれば　aもbも出せます

やはり一番計算するのは3番目のcとθがわかっている時にbを求めるのが

現場では多いかもですね。

研磨機のサインチャックやサインドレッサーに名前の通りのサインバー

精密サインバイスなんてのも御座いますね

弊社にもそんなの沢山有りますよっ

それがコチラ↓　ハイ！ドーン

中古機械・中古工作機械情報　～　工作機械の遠藤機械工業です / 全商品 (endokikai.com)

三角関数を使って計算する事を習ってこなかった人には難しいかな～

やっぱ携帯のアプリが簡単だわと思ってしまうリーゼント印